n

NintroductionnN důležitý směr v vibračních diagnostice leteckých plynových turbínových motorů a turbomachines jenndiagnostiky prostřednictvím modelování. Modelování dává příležitost spojit přítomnostněkterých druhů strojních defektů s příznaky jeho přítomnosti v vibračním signálu. Jedním z takových defektů je vzhled trhlin v hřídeli leteckých motorů a turbomachinů, které jsounepříznivé. Takženejdůležitějším úkolem diagnostického systému je detekovat trhlin včas a předpovídat jeho pokrok.n

nappearance trhliny v rotoru má zanásledek snížení lokální tuhosti. Hodnota ztráty tuhosti závisína geometrických charakteristikách trhliny. Pokud se aplikuje statické zatížení, jako je hmotnostní síla, sejde a zavře se, když se rotor otáčí. V důsledku toho se změní tuhost hřídelena cyklus. Prasknutí v rotorovém systému vede ke změnámn

nnfolloňování změn vibračního signálu [1]:n statického vychýlení způsobeného snížením tuhosti.nn ·n ·n ·nPapearance 2x složky otáčení rychlosti díky asymetrické tuhosti rotoru.nn ·n ·n ·nPapearance 3х složky otáčení v důsledku cyklického otvoru a zavírání trhliny.n Hlavním úkolem matematického modelu je popis hodnoty a práva lokální změny v tuhosti vndnN101; Crack probíhá conejvíce faktorů.nN-n Nere jsouněkolik přístupů ke simulaci trhliny. Vnejjednodušších případech je trhlina simulována poklesem radiální tuhosti celého hřídele [2,3,4]. V ostatních případech hřídelová část, kden101; Crack probíhá, jenahrazenn101; D o ekvivalentní prvek paprsku. Koeficienty matice z tuhosti takového prvku jsou vypočteny s trhlinami v úvahu a měnitna cyklus. V práci [5] Výpočet matice tuhosti prvkunosníku s trhlinou je založenna použití setrvačných momentů sekce paprsku zvažuje trhliny. V práci [6] se ztuhlost matrice takového prvku vypočítána základě rovnic mechaniky zničení pevných těles. Trhlina může být simulována elastickým spojem spojujícím hraniční části hřídele v místě jeho umístění a dávat tuhost momentu trhliny [7,8].n

nChange v tuhosti trhliny v závislostina jeho otevírání a zavírání, zatímco rotor se může být popsán matematicky různými způsoby. Vnejjednodušším případě se může předpokládat, že trhlina má pouze dvě pozice: zcelan

Nnocnocinebo zcela uzavřené a kroková funkce může být použita k popisu jeho tuhosti změna matematicky [4]n.nn N práci [3] popisujenejzajímavější modely změny tuhosti. Jedním znich je gaschová rovnice. Změnann Nevzničnost se provádí v závislostina úhlu mezi fází statické síly a fáze trhlin a popsaným 17 harmonickými fourierovými sériemi. Stejný článek dává Maesn davies rovnice whern101; Ztuhlost se mění v závislostina úhlu podle kosinového práva. V ztuhlosti modelu jangu se změní v důsledku kosinového zákona ve stupni relativní hloubky trhliny.ntis Článek vyvíjí model trhlinyna základěn

To dává příležitost zvýraznit známky používané k detekci jeho stavu pro přesný rotor.n

N ilgoritmus je zahrnut do softwarového programu Dynamics R4 [9], který představuje vyhrazený NSSystemna výpočet dynamického chování komplexních systémů rotoru.nnnccrackový model koeficienty. Pokudneexistuje žádná trhlina, je splněna stav kompatibility deformace mezi sekcemi dílů hřídele, takže všechny vzájemné posuny jsou zakázány. Zavedeme rotující souřadný systém ηoε ležící v oblasti trhliny, obrázek 1. jeho původ se shoduje s původem pevného souřadného systému XYZ. Hřídel provádí dva pohyby - správná rotace a precese kolem osy z. Při popisu trhliny považujeme pouze otáčení kolem η a ε os. Vymítnutí v jiných stupních svobody jsou zanedbány. Nnn

n

nnnnfigure 1. crack sekcennn

NFlexibility MATRIX LINKU Simulace trhlin v systému otočného souřadnic může být zapsána jakon

nfollowing:nnnnn

n

nndern101;nnqn

n

N rozdílu v fázích,n&n#Úhel otáčení hřídele,nn

n

nPředchozí úhel pro precion;n&ngn#n&(nqnq ) annq#)n (nqn)n

)n

ncoefficenci momentu flexibilitan. \\ tnnn nnnndnflexicity závisína úhlunqnqnqusause, zatímco hřídel se otáčí, se otevře a zavře se trhliny. Matice ztuhlosti se získá inverzímn(nqnn (nqn)n)nMatrix anulové koeficienty flexibility Hlavní diagonální vedení k získání koeficientů ztuhlosti, které jdou donekonečna. Omezňujeme hodnotu takových koeficientů tuhosti o 1е10nnm; Tento předpoklad významněneovlivní výsledek, tj. Získámennn

n

nNásledná rovnice:nn

n

n&6n101;n&[n#]n]n]nn

n Rotační matice (4), kden101;n

ncnnncos (ndn ),nnnnnsin (nndn).nn

n

násnásobící matice v souladu s rovnicí (3) Získáme:n

nnn

n

n) Provádímeněkteré transformace, které dávají příležitost přecházetna jednodušší popis trhlinynstiffness matrice a algoritmus získávání koeficientů. V souladu s modelem MAES se předpokládá, že se předpokládá, že radiální flexibilita kruhového paprsku se změnami trhlin z minima do maximální hodnoty Cosine Law. \\ TnNnn

n n6n101;n

N0n0n

pružnostnosníku bez crack (minimální hodnota),ngcnn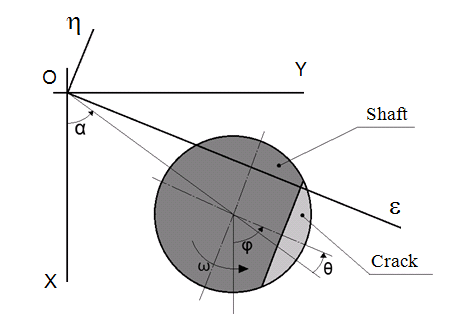n

flexibilitunosníku s otevřenýminncrack (maximální hodnota). \\ tn

n n n n) vyměnit crack pomocí závěsu s momentem tuhostn n

n

nnn

n

nn n n. Podmínky okrajů paprsku by měly poskytovat své definovatelnost, jak je uvedenona obrázku 2.n nnnn . Výměna trhlin pomocí závěsun

n

nnnn

n

nnder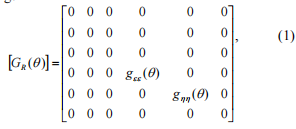101;nn
m mladý modul,n

nnmhn

- koeficient momentové tuhosti ekvivalentní propojení odpovídající plně otevřené trhliny.nn n nnnn&n#n nnn nnn=